chevron_left
Back to "Mathematics > Cross Sums"
Continue to "Mathematics > x^x Mathematics"
chevron_right03-30-2003
Square root approximation
For a long time I played around with formulas for fun and even today I still use some algebraic transformations that are not really considered to be equivalent. Of course, very often only nonsense comes out of it. However, there are also exceptions, so that a small mistake in the transformation leads to a completely different formula, which is basically good for the same thing, but serves a slightly different purpose. At some point I got the idea that I don't always want to calculate square roots with calculators, instead I want to be able to approximate them correctly in my head. My efforts started with a not quite optimal formula, in which two square numbers (a^2 and b^2, a and b as element of the integers (1, 2, 3, ...)) are necessary in addition to the number to be determined - one lower than the sought number, the other one higher - which served as orientation, so to speak, in order to be able to calculate the root of a number lying in between. The formula of the sought root w was at the time:
w = √a + (x - a)/(b - a)
Soon after, I noticed that the part (b-a) can always be reformulated relative to a, making the variable b superfluous. One plus twice the root of a corresponded exactly to b-a, so the formula could easily be modified. Now, however, I wanted to keep the formula as simple as possible, so I simply omitted the "1+" in the denominator of the fraction, which is one of the not quite equivalent transformations:
w = √a + (x - a)/(2*√a)
Although this increased the calculation error of the approximation formula, the formula was now simpler overall.
A few days later I noticed that the true root in each case lies somewhere between the two root approximations above - so I could combine both formulas and take their average value, which would ultimately be a lot more accurate. By using the following formula, I had at least managed to get the first decimal place correct most of the time, and the second decimal place correct in some cases as well:
w = [2*√a + (x - a)/(b - a) + (x - a)/(2*√a)] / 2
Now I once again had two additional orientation variables - I didn't immediately remember, but didn't I once mention something about the fact that (b-a) can be formulated relative to a? In principle, this corresponds exactly to the denominator of the other fraction, except that 1 is simply added to the first fraction. So we get:
w = [2*√a + (x - a)/(2*√a+1) + (x - a)/(2*√a)] / 2
Now we can apply the 2 at the end of the formula, which in correct mathematical formulation should be below the fraction line of the term inside the square brackets, to all three summands individually:
Now the question arises whether one cannot shorten this exact AND unfortunately quite long formula somehow. Here now one of my proven trying-methods was used, which after a lot of trial and error changed the equation as follows:
w = √a + 4(x - a)/(8*√a + 2)
And you can shorten this one quite nicely...
w = √a + (x - a)/(2*√a + 0.5)
Nice short formula, but why the heck does it have to add +0.5 for it to be so accurate? Would 0.33 or 0.67 possibly be more accurate? I called this number z and finally made a list to see which z leads to the best root approximation. The amazing thing was: which number you use instead of 0.5 doesn't matter at all, as long as you replace the 0.5 with the new result and calculate the whole thing again. This can be done even more often and so finally the root can be calculated as accurately as you want.
Through a lot of trial and error, which consumed a good 4 A4 pages, I finally managed to simplify this so-called iteration (stepwise approximation) considerably - it now no longer contains roots and reads:
Z1 = 1 + (x - 1)/(Z0 + 1)
This again, although already very simple, can be simplified even further. To my shame, I must confess that I haven't looked at the formula for almost 2 years - afterwards I saw right away that it must be possible to simplify it even more. The result was the following:
Zn+1 = (Zn + x)/(Zn + 1)
A wonderfully simple iteration for root calculation - although it is only valid for the calculation of second roots, i.e. of square roots, it only contains the four basic arithmetic operations compared to Newton's iteration of arbitrary roots. As I found out later, Newton's iteration is more complicated and even contains the power (n-1) once:
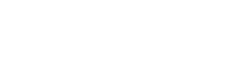
Compared to the simple iteration for second roots, Newton's iteration is quite complicated in my opinion. On the other hand, it is able to iterate any root from any number with arbitrary precision.
What I would like to know now: is it possible to somehow derive my iteration from Newton's iteration? Maybe it is possible, but maybe are fundamentally different - if you want to try to derive or to prove that the iterations are different, please do so. Provided that there are no contradictions, I would love to include the derivation, the proof or a disproving proof here at any time.
As far as mental arithmetic of roots goes, I ultimately settled on the simplest one-step formula:
w = √a + (x - a)/(2*√a)
If you now start to learn this formula by heart, you will soon realize that it is much easier to remember than you initially think. Let me demonstrate with an example: if you want to calculate root 19, you take the next best square number, 16. Since root 19 lies between root 16 (4^2) and root 25 (5^2), you know that it must have a 4 before the decimal point, which is what the root of this next best square number, in this case 16, serves for. Now for the decimal places, and here a simple fraction is good - how far is 19 from 16? Exactly 3, which is what we put above the fraction line. Now another arbitrary-sounding value: two times the next best root (root of 16 is 4), in this case 2*4 = 8, which we put under the fraction bar. So we have approximately 4 + 3/8, which you can leave as a solution if you don't want to convert the fraction to decimal. As a decimal number, the fraction is 4.375 - the true root of 19 is 4.3589..., which means we are quite close.
To give another example, what is the square root of 29? The next best square numbers are 25 and 36, let's just take the larger one here - to show that it works just as well with that. The root of the next highest number is 6, so the number before the decimal point of the root we are looking for must be one less, so 5. How far is 29 from 36? Exactly, 29 is smaller by 7. Now again double the root of the next best square number, that is 2*6, which makes 12. So the root is approximately 6 + (-7)/12 or also 6 - 7/12, which is approximately between 5.4 and 5.5. The true root is 5.385..., which is related to the fact that we took a next best square number that was a little further away, by 7 numbers. The real closest square number would have been 25, which is only 4 numbers away. The result with that would be 5 + 4/10, which is 5.4 - that's a more accurate result, which is basically rounding the true root. So the farther away the next best square number is, the larger the approximation error becomes - but in most cases this should be bearable, if you don't want to precisely calculate the first 100 decimal places of a square root. :-) And in that case there is the already mentioned, simplest square root iteration in the world with x as variable standing for the searched root:
Zn+1 = (Zn + x)/(Zn + 1)
w = √a + (x - a)/(b - a)
Soon after, I noticed that the part (b-a) can always be reformulated relative to a, making the variable b superfluous. One plus twice the root of a corresponded exactly to b-a, so the formula could easily be modified. Now, however, I wanted to keep the formula as simple as possible, so I simply omitted the "1+" in the denominator of the fraction, which is one of the not quite equivalent transformations:
w = √a + (x - a)/(2*√a)
Although this increased the calculation error of the approximation formula, the formula was now simpler overall.
A few days later I noticed that the true root in each case lies somewhere between the two root approximations above - so I could combine both formulas and take their average value, which would ultimately be a lot more accurate. By using the following formula, I had at least managed to get the first decimal place correct most of the time, and the second decimal place correct in some cases as well:
w = [2*√a + (x - a)/(b - a) + (x - a)/(2*√a)] / 2
Now I once again had two additional orientation variables - I didn't immediately remember, but didn't I once mention something about the fact that (b-a) can be formulated relative to a? In principle, this corresponds exactly to the denominator of the other fraction, except that 1 is simply added to the first fraction. So we get:
w = [2*√a + (x - a)/(2*√a+1) + (x - a)/(2*√a)] / 2
Now we can apply the 2 at the end of the formula, which in correct mathematical formulation should be below the fraction line of the term inside the square brackets, to all three summands individually:
| [1] | 2*√a : 2 | = | √a |
| [2] | (x - a)/(2*√a + 1) : 2 | = | (x - a)/(4*√a + 2) |
| [3] | (x - a)/(2*√a) | = | (x - a)/(4*√a) |
| --> | w | = | [1] + [2] + [3] |
| --> | w | = | √a + (x - a)/(4*√a) + (x - a)/(4*√a + 2) |
Now the question arises whether one cannot shorten this exact AND unfortunately quite long formula somehow. Here now one of my proven trying-methods was used, which after a lot of trial and error changed the equation as follows:
w = √a + 4(x - a)/(8*√a + 2)
And you can shorten this one quite nicely...
w = √a + (x - a)/(2*√a + 0.5)
Nice short formula, but why the heck does it have to add +0.5 for it to be so accurate? Would 0.33 or 0.67 possibly be more accurate? I called this number z and finally made a list to see which z leads to the best root approximation. The amazing thing was: which number you use instead of 0.5 doesn't matter at all, as long as you replace the 0.5 with the new result and calculate the whole thing again. This can be done even more often and so finally the root can be calculated as accurately as you want.
Through a lot of trial and error, which consumed a good 4 A4 pages, I finally managed to simplify this so-called iteration (stepwise approximation) considerably - it now no longer contains roots and reads:
Z1 = 1 + (x - 1)/(Z0 + 1)
This again, although already very simple, can be simplified even further. To my shame, I must confess that I haven't looked at the formula for almost 2 years - afterwards I saw right away that it must be possible to simplify it even more. The result was the following:
Zn+1 = (Zn + x)/(Zn + 1)
A wonderfully simple iteration for root calculation - although it is only valid for the calculation of second roots, i.e. of square roots, it only contains the four basic arithmetic operations compared to Newton's iteration of arbitrary roots. As I found out later, Newton's iteration is more complicated and even contains the power (n-1) once:
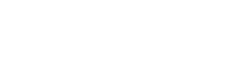
Compared to the simple iteration for second roots, Newton's iteration is quite complicated in my opinion. On the other hand, it is able to iterate any root from any number with arbitrary precision.
What I would like to know now: is it possible to somehow derive my iteration from Newton's iteration? Maybe it is possible, but maybe are fundamentally different - if you want to try to derive or to prove that the iterations are different, please do so. Provided that there are no contradictions, I would love to include the derivation, the proof or a disproving proof here at any time.
As far as mental arithmetic of roots goes, I ultimately settled on the simplest one-step formula:
w = √a + (x - a)/(2*√a)
If you now start to learn this formula by heart, you will soon realize that it is much easier to remember than you initially think. Let me demonstrate with an example: if you want to calculate root 19, you take the next best square number, 16. Since root 19 lies between root 16 (4^2) and root 25 (5^2), you know that it must have a 4 before the decimal point, which is what the root of this next best square number, in this case 16, serves for. Now for the decimal places, and here a simple fraction is good - how far is 19 from 16? Exactly 3, which is what we put above the fraction line. Now another arbitrary-sounding value: two times the next best root (root of 16 is 4), in this case 2*4 = 8, which we put under the fraction bar. So we have approximately 4 + 3/8, which you can leave as a solution if you don't want to convert the fraction to decimal. As a decimal number, the fraction is 4.375 - the true root of 19 is 4.3589..., which means we are quite close.
To give another example, what is the square root of 29? The next best square numbers are 25 and 36, let's just take the larger one here - to show that it works just as well with that. The root of the next highest number is 6, so the number before the decimal point of the root we are looking for must be one less, so 5. How far is 29 from 36? Exactly, 29 is smaller by 7. Now again double the root of the next best square number, that is 2*6, which makes 12. So the root is approximately 6 + (-7)/12 or also 6 - 7/12, which is approximately between 5.4 and 5.5. The true root is 5.385..., which is related to the fact that we took a next best square number that was a little further away, by 7 numbers. The real closest square number would have been 25, which is only 4 numbers away. The result with that would be 5 + 4/10, which is 5.4 - that's a more accurate result, which is basically rounding the true root. So the farther away the next best square number is, the larger the approximation error becomes - but in most cases this should be bearable, if you don't want to precisely calculate the first 100 decimal places of a square root. :-) And in that case there is the already mentioned, simplest square root iteration in the world with x as variable standing for the searched root:
Zn+1 = (Zn + x)/(Zn + 1)